Historien om Malcolm X
2024-04-24 12:00
VALFUSK. Benfords lag är en matematisk lag som används för att bekämpa brott och manipulerade skeenden. Beräkningar med modellen visar att Demokraterna i USA har bedrivit omfattande valfusk.
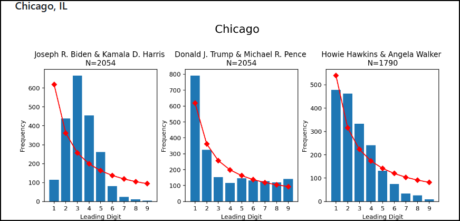
Benfords lag visar att det har bedrivits omfattande valfusk i vissa stater, medan andra stater uppvisar normalt röstande. Valfusket har koncentrerats till stater där det behövts för att Joe Biden skulle vinna valet. Klicka på bilden för att komma till GitHub där fler data och grafer presenteras.
Politiker ljuger ofta, men det gör inte matematik. Benfords lag, även kallad Newcomb–Benford-lagen, lagen om avvikande nummer, eller förstasifferslagen, är en iakttagelse om frekvensfördelningen av ledande siffror i många verkliga uppsättningar av numeriska data.
Benfords lag används för ett oräkneligt antal syften av försäkringsbolag för att avslöja bedrägerier, poliser för att avslöja brott, skatteverket för att avslöja skattebedrägerier, med mera.
Förenklat kan sägas att Benfords lag visar att i naturligt förekommande samlingar av siffror, är den ledande siffran sannolikt liten.
Vid exempelvis bildanalys, kan man med Benfords lag mäta förekomsten av en bilds färginnehåll och bildelementsförekomst, och jämföra utfallet med hur bilden skall se ut enligt Benfords lag. Om en bilds komponenter på ett avgörande sätt avviker från Benfordfördelningen, förstår man att bilden är manipulerad.
Om detta berättar programledaren Latif Nasser i fjärde episoden av den amerikanska vetenskapsdokumentärserien Connected: The Hidden Science of Everything, avsnitt ”Digits” (serien finns även svensktextad hos kommersiella videoströmningstjänster):
Om en stor datamängd avviker mycket från Benfords lag kan det vara en indikation på att siffrorna kan vara påhittade eller manipulerade. Detta gör lagen praktiskt användbar för kontroll inom många skilda områden. Som exempel är lagen tillämplig vid ekonomisk redovisning, prislistor, antal röster vid omröstningar mellan ett stort antal alternativ, som med många presidentkandidater och senatorer, samt folkmängd i städer.
Om siffrorna fördelades enhetligt, skulle varje siffra uppstå omkring 11.1 procent av gångerna. Benfords lag gör också förutsägelser om fördelningen av andra siffror, tredje siffror, sifferkombinationer, och så vidare.
Enkelt kan sägas, att i uppsättningar som lyder lagen, visas siffran 1 som den ledande signifikanta siffran i cirka 30 procent av fallen, medan 9 förkommer med mindre än fem procents frekvens.
Lagen säger till exempel att siffran 1 bör vara förstasiffra i 30,1 procent av fallen, siffran 2 i 17,6 procent av fallen och siffran 9 i 4,6 procent av fallen i en stor datamängd.
Wikipedia ändrar sig – massmedier håller tyst
Den engelskspråkiga Wikipediasidan om Benfords lag redigerades på lördagen, en dag efter det att de data publicerades som ligger till grund för Benfordsberäkningarna bakom de grafer som denna artikel länkar till.
Den 15 januari beskrev Wikipedias artikel hur Benfords lag använts för att avslöja valfusk i Iran, medan artikeln samtidigt angav att ”andra experter” anser att Benfords lag är oanvändbar vid valfusksanalyser.
I den av Wikipedia på lördagen reviderade artikeln, nämns inte längre att metoden använts för att avslöja valfusk i Iran. Nu står det att metoden inte är ”idiotsäker” och att tre namngivna statsvetare – alltså inte matematiker eller statistiker – anser att metoden är ”problematisk” och ”vilseledande” vid studier av valfusk.
Ändå används Benfords lag mycket flitigt vid just undersökningar av bedrägerier. Som Latif Nasser berättar i sin ovan presenterade dokumentärserie, är beräkningsmetoden så kraftfull ”att den amerikanska regeringen inte ens vill att vi ska känna till den”, vilket till exempel gäller det ”amerikanska” skatteverket IRS.
De studier som presenterats av hittills räknade röster, visar att Joe Biden har vunnit folkets röster genom omfattande valfusk.
Om amerikanska myndigheter, politiker eller massmedier kommer att bry sig om de matematiska indicierna och bevisen på valfusk till Joe Bidens fördel, är en helt annan fråga som framtiden måste utvisa.